激活函数
Sigmoid
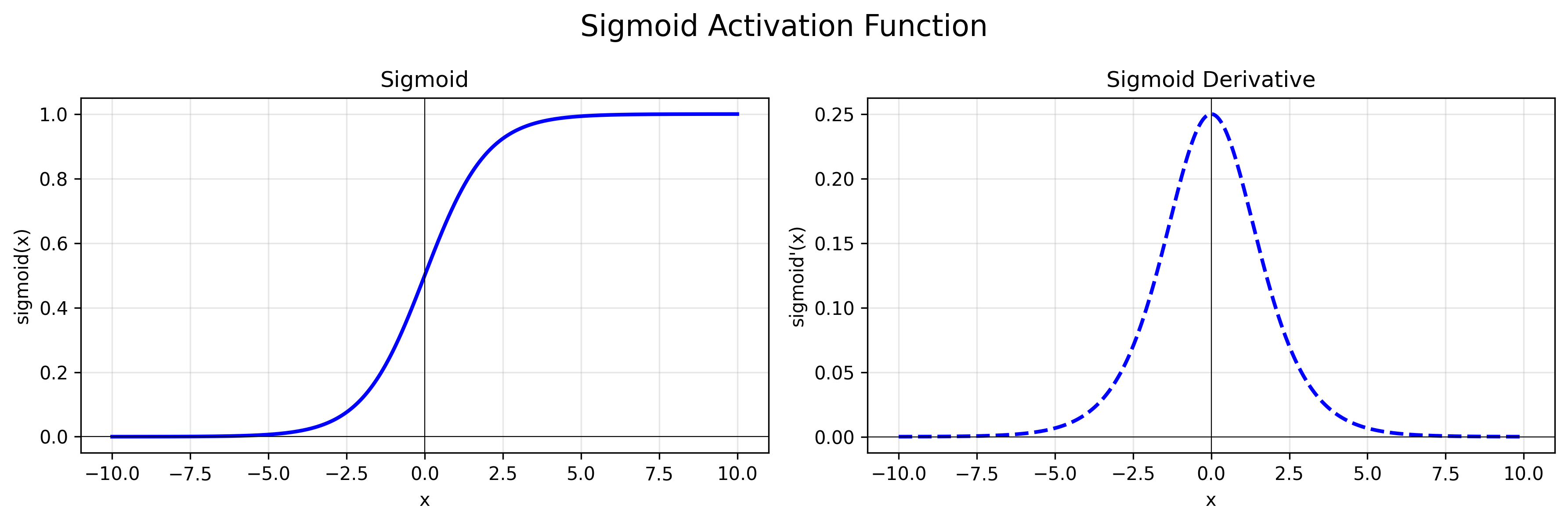
公式：$f(x) = \frac{1}{1 + e^{-x}}$
导数：$f’(x) = f(x) * (1 - f(x))$
特点：函数输出在(0,1)之间，导数输出在(0,0.25)之间。[-6, 6]之间比较敏感，[-3, 3]之内效果较好。一般5层之内就会出现梯度消失现象，一般只用于二分类的输出层。
Tanh
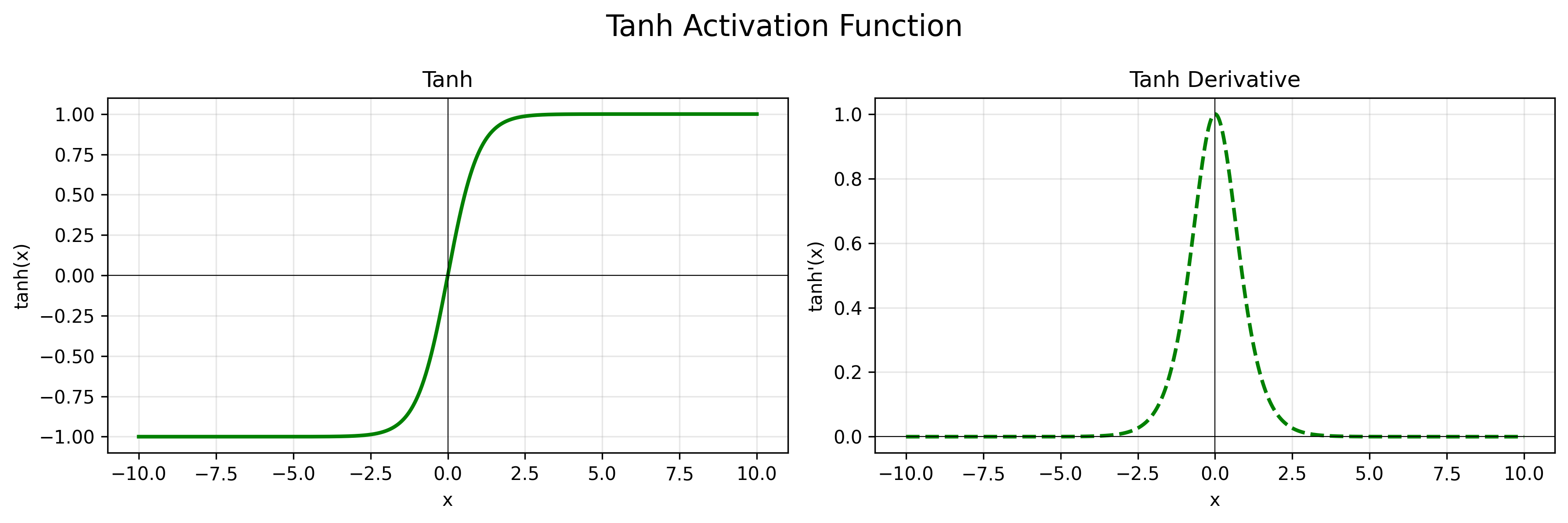
公式：$f(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$
导数：$f’(x) = 1 - f(x)^2$
特点：函数输出范围在(-1, 1)之间，导数输出在(0,1)之间。收敛速度更快，一般用于隐藏层。
ReLU（Rectified Linear Unit）
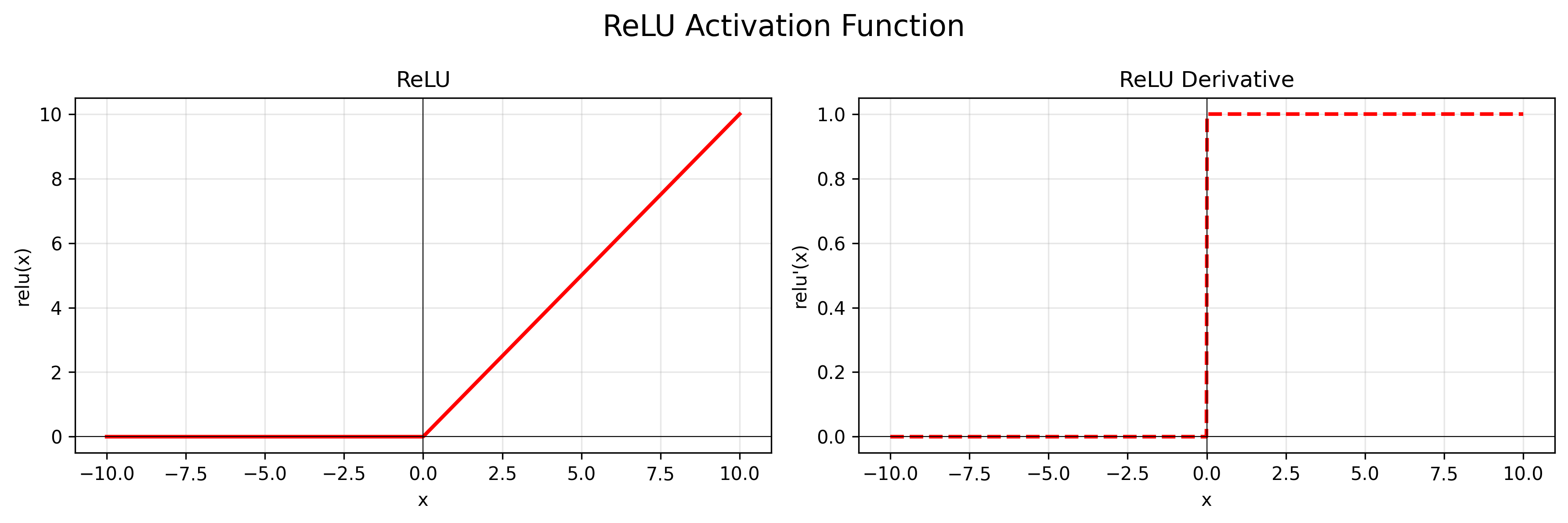
公式：$f(x) = max(0, x)$
导数：$f’(x) = 1$ if $x > 0$; $f’(x) = 0$ if $x < 0$
特点：忽略负信号，更简单，效率更高。会使一部分神经元输出为0，减少参数之间的依存关系，缓解过拟合。一般隐藏层首选。
为了考虑负样本所以有了 PReLU（Parametric ReLU）：
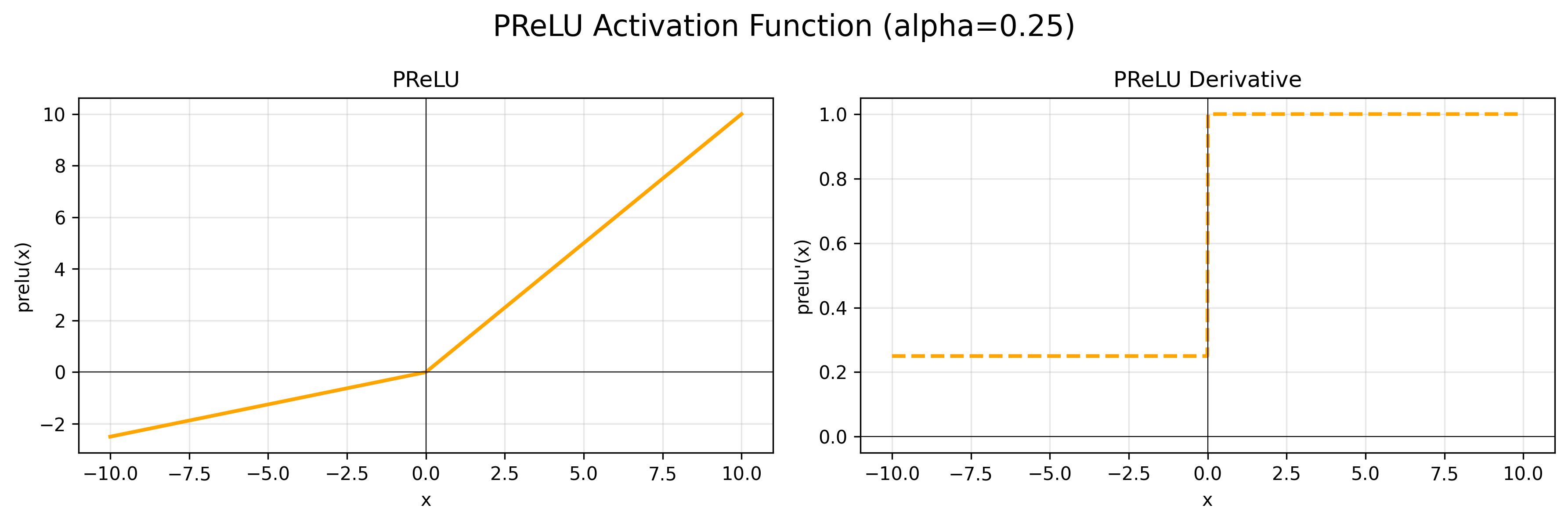
公式：$f(x) = max(0, x) + \alpha * min(0, x)$
导数：$f’(x) = 1$ if $x > 0$; $f’(x) = \alpha$ if $x < 0$
当 $\alpha$ 取 0.01 时，也叫 Leaky ReLU。
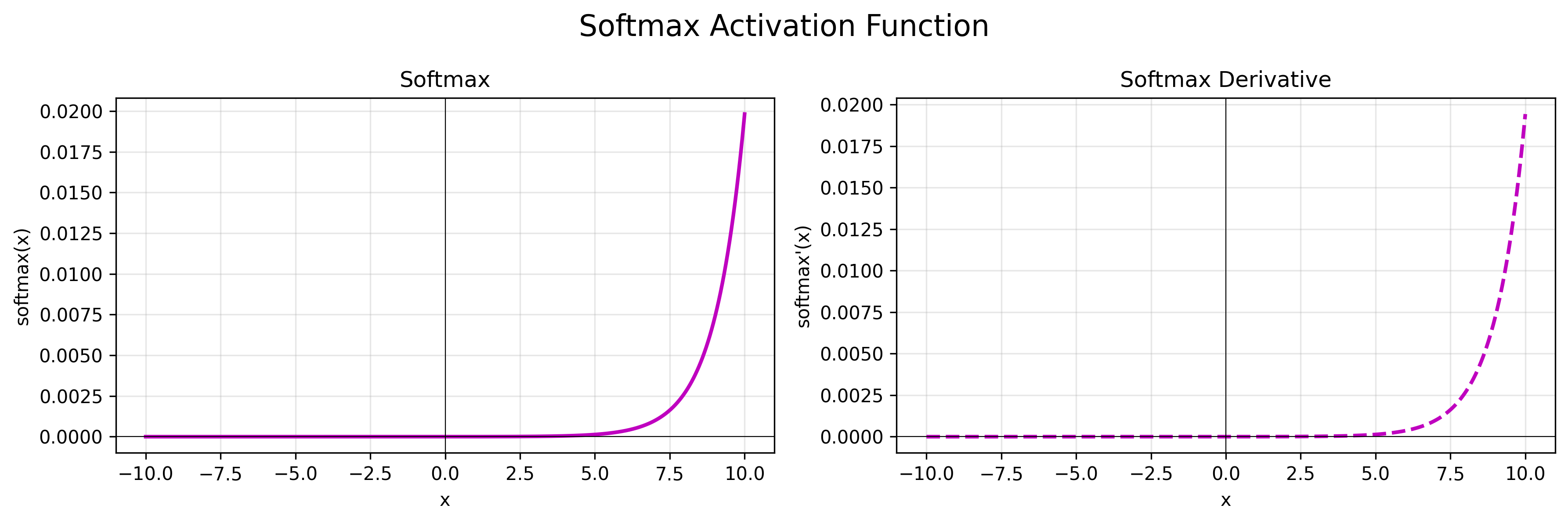
Sofmax
公式：$f(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{n} e^{x_j}}$
导数：$f’(x_i) = f(x_i) * (1 - f(x_i))$
特点：将多分类结果按照概率输出，适用于多分类的输出层。
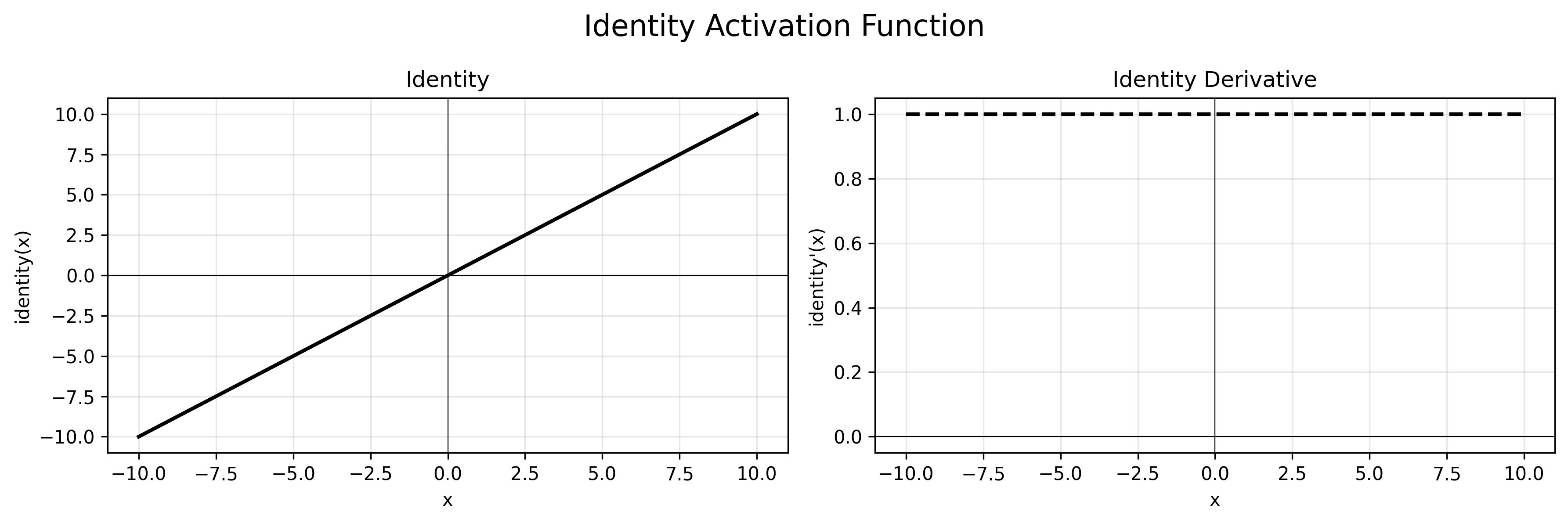
Identity
公式：$f(x) = x$
导数：$f’(x) = 1$
特点：无激活函数，直接输出，适用于回归任务。
激活函数的选取规则：
-
隐藏层：ReLU -> Leaky ReLU / PReLU -> Tanh -> Sigmoid
-
输出层：二分类 -> Sigmoid；多分类 -> Softmax；回归 -> Identity
参数初始化
- 均匀分布：从区间均匀随机取值，默认区间 (0, 1)，可以设置为 $(-\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}})$，其中 n 是输入的维度。可以打破对称性，防止神经元输出相同。但是随机范围不当可能会导致梯度问题。适用于浅层网络或者低复杂度模型。
- 正态分布：随机从均值为0，标准差为1的高斯分布中取样，使用很小的值进行初始化。
- 全 0/1：全设置为 0/1。实现简单，但是不能打破对称性。全 1 会导致激活值指数增长，梯度爆炸。
- 固定值：权重参数初始化为固定值。实现简单，但是不能打破对称性。
- kaiming 初始化：也叫 HE 初始化，适用于 ReLU 激活函数。
- 正态分布：从 [0, std] 中取样，其中 $std = \sqrt{\frac{2}{fan_{in}}}$
- 均匀分布：从 [-limit, limit] 中取样，其中 $limit = \sqrt{\frac{6}{fan_{in}}}$
- $fan_{in}$：输入的维度
- Xavier 初始化：也叫 Glorot 初始化，使用于Sigmoid 和 Tanh 激活函数。
- 正态分布：从 [0, std] 中取样，其中 $std = \sqrt{\frac{2}{fan_{in} + fan_{out}}}$
- 均匀分布：从 [-limit, limit] 中取样，其中 $limit = \sqrt{\frac{6}{fan_{in} + fan_{out}}}$
- $fan_{in}$：输入的维度
- $fan_{out}$：输出的维度
损失函数
多分类交叉熵损失
公式：$L = -\sum_{i=1}^{N} y_i \log (S(f_{\theta}(x_i)))$
- $y_i$ 样本属于某个类别的真实概率（0/1）
- $f(x_i)$ 样y属于某一类别的预测分数
- $S$ softmax 函数，将预测分数转换为概率分布
二分类交叉熵损失
公式：$L = -y \log \hat{y} - (1 - y) \log (1 - \hat{y})$
- $y$ 样本属于某个类别的真实概率（0/1）
- $\hat{y}$ 样本属于某个类别的预测概率，需要通过 sigmoid 函数转换为概率分布
MAE (L1 Loss)
公式：$L = \frac{1}{N} \sum_{i=1}^{N} |y_i - \hat{y}_i|$
- $y_i$ 样本的真实值
- $\hat{y}_i$ 样本的预测值
须有稀疏性，惩罚较大的值。梯度在零点不平滑，跳过极小值。
MSE Loss
公式：$L = \frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2$
常常作为正则项，预测值和目标值相差很大时会造成梯度爆炸。
Smooth L1 Loss
公式：
综合 MAE 和 MSE，解决 L1 不光滑和离群点梯度爆炸的问题。
梯度下降优化方法
指数加权平均公式：
- $S_t$ 表示 $t$ 时刻的指数加权平均
- $Y_t$ 表示 $t$ 时刻的值
- $\beta$ 表示衰减系数，取值范围 $0 < \beta < 1$，越大数据越平缓
动量算法 Momentum
梯度计算公式：$s_t = \beta s_{t-1} + (1 - \beta) g_t$
更新公式：$w_t = w_{t-1} - \eta s_t$
- $s_t$ 表示 $t$ 时刻的指数加权平均梯度值
- $g_t$ 表示 $t$ 时刻的梯度
- $\beta$ 调节权重系数
- $\eta$ 表示学习率
- $w_t$ 表示 $t$ 时刻的模型权重参数
Adagrad
- 初始化学习率 $\eta$、初始化参数 $w$、小常数 $\sigma = 10^{-10}$
- 初始化梯度累计变量 $s = 0$
- 从训练集中采样 $m$ 个样本的小批量，计算梯度 $g_t$
- 累积平方梯度：$s_t = s_{t-1} + g_t \odot g_t$，其中 $\odot$ 表示各个分量相乘
- 学习率更新公式：$\eta = \frac{\eta}{\sqrt{s_t} + \sigma}$
- 权重参数更新公式：$w_t = w_{t-1} - \frac{\eta}{\sqrt{s_t} + \sigma} \cdot g_t$
- 重复步骤 3–7
缺点：学习率过早过量降低，训练后期学习率太小，难以找到最优解。
RMSprop
对 Adagrad 的改进，计算梯度时使用指数平均加权。
梯度计算公式：$s_t = \beta s_{t-1} + (1 - \beta) g_t \odot g_t$
学习率计算公式：$\eta = \frac{\eta}{\sqrt{s_t} + \sigma}$
权重参数更新公式：$w_t = w_{t-1} - \frac{\eta}{\sqrt{s_t} + \sigma} \cdot g_t$
Adam
将 Momentum 和 RMSprop 结合起来，计算梯度的一阶矩（平均值）和二阶矩（梯度的方差）的自适应估计：
- 修正梯度：使用梯度的指数加权平均
- 修正学习率：使用梯度平方的指数加权平均
梯度计算公式：
$$ \begin{align*} m_t &= \beta_1 m_{t-1} + (1 - \beta_1) g_t \ s_t &= \beta_2 s_{t-1} + (1 - \beta_2) g_t^2 \ \hat{m}_t &= \frac{m_t}{1 - \beta_1^t}, \quad \hat{s}_t = \frac{s_t}{1 - \beta_2^t} \end{align*} $$
权重参数更新公式：
$$ w_t = w_{t-1} - \frac{\eta}{\sqrt{\hat{s}_t} + \epsilon} \hat{m}_t $$
- $m_t$ 是梯度的一阶矩估计
- $s_t$ 是梯度的二阶矩估计
- $\hat{m}_t$ 和 $\hat{s}_t$ 是偏差校正后的估计
学习率衰减策略
等间隔衰减
每隔一定周期，将学习率按固定比例衰减。例如每 50 epoch，衰减 0.5，学习率变化如图所示：
指定间隔衰减
手动指定每隔多少间隔按比例衰减。例如按照图中 milestones 每次衰减 0.5，学习率变化如图所示：
指数衰减
学习率按指数衰减。例如每 epoch 衰减 0.95，学习率变化如图所示：
余弦退火
学习率随训练周期变化，类似于余弦函数。公式如下：$\eta_t = \eta_{\text{min}} + \frac{1}{2} (\eta_{\text{max}} - \eta_{\text{min}}) \left(1 + \cos\left(\frac{T_{\text{cur}}}{T_{\text{max}}} \pi\right)\right)$
- $\eta_{\text{min}}$ 是学习率的最小值（通常为 0）
- $\eta_{\text{max}}$ 是学习率的初始值
- $T_{\text{cur}}$ 是当前的训练周期内的步数
- $T_{\text{max}}$ 是单个训练周期内的步数
正则化
Dropout
训练过程中，随机将部分神经元的输出置为 0，防止过拟合。dropout 率为 $p$，则每个神经元被置为 0 的概率为 $p$，通常为0.2到0.5之间。实际应用中通常在全连接层后增加 Dropout 层。
批量归一化 (Batch Normalization)
先对数据标准化，再对数据重构：
$$ f(x) = \lambda \cdot \frac{x - E(x)}{\sqrt{Var(x)} + \epsilon} + \beta $$
- $\lambda$ 和 $\beta$ 是可学习的参数，用于重构数据
- $E(x)$ 是 $x$ 的均值
- $Var(x)$ 是 $x$ 的方差
- $\epsilon$ 是一个小的常数，用于防止除以零
CNN
卷积神经网络 (Convolutional Neural Network, CNN) 是含有卷积层的神经网络，主要由三部分构成：
- 卷积层：负责提取图像中的局部特征
- 池化层：用来大幅降低参数量级（降维）
- 全连接层：用来输出结果
卷积层
卷积层（Convolutional Layer）通t卷积操作提取输入数据中的特征。利用卷积核对输入处理，从而生成特征图，并且每个卷积层能够提取到不同层次的信息，从低级特征到高级特征。
卷积运算：卷积核和输入数据的局部区域间做点积（对应位置相乘再求和）
卷积层作用：
- 特征提取：从输入图像中提取低级特征（边缘、角点、纹理等），通过多个卷积层堆叠，网络能够逐渐从低级特征到高级特征（物体的形状、区域等）进行学习
- 权重共享：同一个卷积核在整个输入图像上共享权重，这使得卷积层的参数量大大减少，减少了计算量并提高了训练效率
- 局部连接：卷积层中每个神经元仅与输入图像的一个小区域相连，这称为局部感受野，这种局部连接方式更符合图像的空间结构，有助于捕捉图像中的局部特征
- 空间不变性：由于卷积操作是局部的并且采用权重共享，卷积层在处理图像时具有平移不变性。也就是说，不论图像出现在图像的哪个位置，卷积层都能有效地检测到这些物体的特征
Padding
Padding：在原图周围增加额外像素（通常是0）
作用：
- 保持空间维度：卷积操作后，空间维度会减小，padding可以防止空间维度减小
- 保留边缘信息：增加边缘像素的计算次数，更好地保留边缘信息
- 提高性能：避免由于特征图尺寸快速缩小而导致的信息丢失
类型：
- Valid：不使用padding，卷积后空间维度会减小。适用于不需要保持尺寸，或者输入图像足够大，边缘信息丢失不重要的情况
- Same：添加足够的填充，卷积后空间维度与输入相同。广泛使用，因为可以保持特征图尺寸，方便网络设计和计算
- Full：添加尽可能多的填充，使得卷积核的每个原书都至少在输入图像上滑动一次，卷积后空间维度会增大。较少使j，因为会增加计算量，并且可能会在边缘引入一些伪影
Stride
Stride：卷积核在图像上滑动时的步伐大小
作用：
- 降低计算复杂度：步长越大则卷积核移动次数越少，降低计算量
- 增大感受野：大步长会增大每个神经元在输入数据上的感受野，能够捕捉更大范围的输入信息
选择：取决于具体应用场景和网络架构。常见为1，尤其是网络的早期层，允许保留更多空间细节。大于1时用于减少特征图尺寸和增大感受野，例如网络后期层需要快速降维时常见设置为2或4。
多通道卷积计算
先对应通道做点积，然后各通道结果相加
多卷积核计算
特征图大小计算
$$ N = \frac{W - F + 2P}{S} + 1 $$
- $N$：特征图大小
- $W$：输入图像大小
- $F$：卷积核大小
- $P$：padding大小
- $S$：stride大小
池化层
降低维度，缓解过拟合，减少计算量和内存消耗
padding:
输入数据为多通道时，池化层对每个输入通道分别池化，不会像卷积层一样相加，所以池化层输入和输出的通道数相等。
RNN
RNN(Recurrent Neural Network)：一种专门处理序列数据的神经网络。
词嵌入层，将文本转换成向量，流程如下：
- 初始化词向量：随机初始化或通过加载预训练的词向量初始化
- 输入索引：每个单词在词汇表里面有一个唯一索引
- 查找词向量：将单词索引映射为对应的词向量
- 输入到RNN：将词向量作为RNN的输入
隐藏状态作用：
- 记忆功能
- 上下文理解
- 连接不同时间步
